INTRODUCCIÓN
La presente investigación tiene como
finalidad medir la relación entre el aprendizaje significativo y la enseñanza
de la matemática, mediante una revisión de documentos científicos, describiendo
destrezas, definiciones y criterios del tema a investigar.
De acuerdo Anzoategui (2021) con
disciplina de la matemática surgió por la necesidad del hombre de administrar
sus recursos relacionados con la agricultura, ganadería, impuestos, comercio,
así como también comprender eventos astronómicos, medir el tiempo, entre otros.
La matemática se encuentra
manifestada en cada aspecto del universo, por ello es necesario que las
personas conozcan aspectos básicos de la disciplina, esta debería ser fácil de
comprender, sin embargo, en la actualidad la enseñanza de la matemática en los
diferentes niveles de educación, suelen ser fuentes de preocupación en padres
de familia, estudiantes e incluso los propios docentes, por lo tanto, es
importante que se desarrolle una enseñanza con enfoque en competencias
adecuadas para una mejor comprensión.
Según Baque Reyes y Portilla Faican
(2021), en el aprendizaje significativo se puede relacionar los conocimientos
nuevos con información previa que el estudiante ya ha adquirido, esto le
permite asignar un significado a lo aprendido para utilizar en otras
situaciones de la vida.
Tipos de aprendizaje significativo
Como plantean Baque Reyes y Portilla
Faican (2021) se presenta la siguiente tipología:
Aprendizaje de representaciones: Se
orienta en la atribución de significados de algunos símbolos.
Aprendizaje de conceptos: Por
ejemplo, un globo o la palabra globo, el individuo aprende mediante un dibujo.
Aprendizaje de proposiciones: Se
capta el significado de ideas que se expresan en forma de proposiciones, es
decir en esta etapa se relaciona las palabras con la construcción de una
oración, de aquí surge un nuevo significado.
Principios y procesos en el
aprendizaje significativo
Según el principio de inclusión, la
nueva información interactúa con los conceptos disponibles en la estructura de
significados del aprendiz, de tal modo que los nuevos conceptos específicos
resultan incluidos en categorías o conceptos más amplios o genéricos,
implicando una modificación enriquecedora de la estructura cognoscitiva del
estudiante (Rivas, 2008).
Estos conceptos más genéricos
denominados inclusores constituyen elementos de anclaje de los nuevos
conocimientos, desempeñando una función fundamental en el aprendizaje
significativo. El concepto de polígono es inclusor de concepto de cuadrilátero,
éste lo es del concepto de paralelogramo, que es inclusor del concepto de
romboide. La nueva información es entendida en función del marco conceptual
disponible, activado en el aprendizaje.
Castillo, Yahuita y Garabito (2006)
mencionan que el aprendizaje se produce sólo cuando se cumplen una serie de
condiciones: que el estudiante sea capaz de relacionar de forma no arbitraria y
sustancial, la nueva información con los conocimientos y experiencias previas
propias o de terceros que tienen en su estructura de conocimientos y que esté
dispuesto a aprender significativamente, además, el contenido de aprendizaje
debe ser potencial o lógico.
Para Guamán (2019) fomentar el
aprendizaje significativo se encuentra el modelo comunicativo-interactivo, este
es un proceso de análisis que formará una participación que lleva a la
socialización de estudiantes y docentes, en el cual se tendrá una perspectiva
de cada uno de ellos, facilitando el proceso de construcción de saberes,
hábitos y habilidades en un ámbito educativo, participativo y colaborativo
Teoría de los campos conceptuales de
Gerard Vargnaud
Desde el punto de vista de Matienzo
(2020).La teoría del campo conceptual sugiere que el aprendizaje significativo
es progresivo, que existe una relación o interacción dialéctica entre la
conceptualización y el dominio de los campos conceptuales, es decir, cuanto más
conceptualiza, más situaciones domina.
Enseñanza de las matemáticas
Teniendo en cuenta a González (2020)
Existen varios recursos didácticos y técnicas, sin embargo, es un problema por
la falta de comprensión de las reglas de numeración decimal posicional, la que
causa problemáticas en la organización del sistema y algoritmos convencionales
de las operaciones. Se han trabajado en estrategias para poder indicar una
mejora en la enseñanza, a través de agrupamientos, utilización de colores
representando unidades, decenas y centenas, pero sigue existiendo problemas ya
que la reforma educativa es tradicionalista.
Según López (2021), los estudiantes
de hoy necesitan un ambiente de aprendizaje que difiera del tradicional,
motivándolos constantemente para que construyan conocimientos matemáticos en el
trabajo diario, aprendiendo de sí mismos las habilidades y capacidades útiles,
por lo tanto, se mejora a sí mismo para enfrentar un mundo cada vez más
exigente, cambiante y globalizado.
Como señala Muñoz (2020) el
enfoque constructivista para la enseñanza aprendizaje de la
matemática conlleva un trabajo grande a los docentes, con el fin de permitir
ideas estandarizadas sobre el área y adoptar una postura constructivista para
guiar un desarrollo de enseñanza, donde el protagonista es el estudiante
considerando sus habilidades, necesidades e intereses
Citando a Vaillant y Zidán (2020)
mencionan que destacar los resultados alcanzados la incorporación del teléfono
celular como el dispositivo que más utilizan los profesores en sus clases de
matemática, en este sentido, los hallazgos coinciden con los resultados de
investigaciones donde se demuestran que los dispositivos móviles devienen en
escenarios educativos nuevos, tanto formales como informales. Si bien la edad
no es un factor que incida en el uso de las tecnologías por parte de los
profesores de matemática participantes en dichos estudios, se halló que otros
factores contextuales como el hecho de disponer de un título de pedagogía para
el nivel donde se desempeñan o la experiencia profesional como profesores de
secundaria son elementos que contribuyen a aumentar la efectividad en el uso de
TIC en Educación Básica.
MATERIAL Y MÉTODOS
El
tipo de investigación aplicada fue descriptiva, según Hernández et al. (2014)
indica que una investigación es descriptiva cuando esta analiza el fenómeno y
los elementos que lo conforman, además de estructurar sus conceptos y delimitar
las variables. Las características subjetivas que surgen a partir de ese tipo
fundamentan el trabajo de manera que el evento determinado quede esclarecido
ante la población a la cual se le esté exponiendo. Para este sentido se realizó
una recopilación de base de datos bibliográficos con respecto al tema a tratar.
Como
el estudio es de tipo documental, quiere decir que esto corresponde a la
metodología empírica de investigación. Las publicaciones, artículos científicos
y referencias de tipo física y digital obtenidas de la biblioteca
universitaria. Habiendo determinado los puntos a revisar, se aplicó un análisis
y síntesis para profundizar en los temas que predominan en la investigación.
Se
utilizó un diseño no experimental, en conjunto con un eje transversal, permitió
al estudio una investigación dentro de un período de tiempo que no posee
seguimiento.
Se
aplicó un cuestionario a 100 estudiantes de nivelación pertenecientes a las
carreras de Psicopedagogía y Turismo de la Facultad de Ciencias Humanas y de la
Educación de la Universidad Técnica de Ambato, los datos obtenidos se
analizaron con el software estadístico SPSS.
RESULTADOS Y DISCUSIÓN
Mediante la
encuesta aplicada “La escala para el aprendizaje significativo y enseñanza de
la matemática” a los estudiantes, se evidenció lo siguiente:
|
Valor
|
gl
|
Chi-cuadrado de Pearson
|
|
9
|
Razón de verosimilitud
|
28,530
|
9
|
Asociación lineal por lineal
|
15,380
|
1
|
N de casos válidos
|
100
|
|
a.
11
casillas (68,8%) han esperado un recuento menor que 5. El recuento mínimo
esperado es ,09
Tabla 1. Prueba de chi cuadrado.
La correlación
empleando la prueba del chi-cuadrado con 9 grados de libertad muestran según el
valor de Pearson una correlación de 30,587ª.
El rendimiento
académico de los estudiantes tiene que ver con aprendizaje significativo que
estos presentan, demostrando así que la enseñanza de la matemática toma parte
de esta relacionándose y permitiendo que los estudiantes de nivelación
promuevan una mejor adaptación y conocimientos teóricos-prácticos de la
materia.
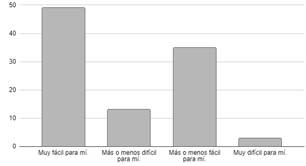
Figura 1. Frecuencia de
percepción en pruebas de matemática.
Nota: Datos tomados de la encuesta.
Se puede
evidenciar que el 49% de las personas encuestadas afirman que es muy fácil resolver
una prueba de matemática, en cambio al 35% les resulta más o menos fácil
resolver la prueba de matemática, un 13% de los estudiantes consideran más o
menos difícil, por consiguiente, el 3% arrojó ser muy difícil para ellos
realizar una evaluación de matemáticas.
DISCUSIÓN
En los
resultados determinados anteriormente se pueden corroborar la correlación
existente entre aprendizaje significativo y enseñanza de la matemática. Esto
debido a que el aprendizaje significativo es el que se arraiga en la memoria a
largo plazo, desde este punto, se enlaza con la enseñanza de la matemática, por
lo que el objetivo es encontrar un medio para que los contenidos de la
aritmética permanezcan en cada uno de los estudiantes. De esta manera se van
construyendo los conocimientos con base en los adquiridos en ciclos anteriores.
|
Dimensiones
de aprendizaje de la matemática
|
Logro
destacado
|
|
Uso
adecuado del lenguaje y la terminología de la matemática
|
22,22
|
|
Asimilación
de las definiciones y conceptos matemáticos
|
30,56
|
|
Dominio
de procedimientos y algoritmos matemáticos
|
30,66
|
|
Asimilación
de afirmaciones y proposiciones matemáticas
|
33,33
|
|
Fortalecimiento
de las demostraciones matemáticas
|
27,78
|
|
Promedio
Porcentual del nivel
|
28,89
|
Tabla 2. Logros del aprendizaje
en matemática
Nota: Información tomada de (Vilchez
Guizado y Ramón Ortiz, 2022)
En el estudio de
Vilchez Guizado y Ramón Ortiz (2022) titulado “Enseñanza flexible y aprendizaje
de la matemática en educación rural”, se evidenció que los estudiantes que
participaron en la muestra se ubican dentro del nivel de logro esperado con un
44,44% del total demuestran un dominio adecuado de lenguaje matemático. Es
decir, el grado de recepción de contenidos es favorable si se considera la
correlación de las variables.
Dentro de la
misma línea de estudio, en el trabajo de Vaillant y Zidán (2020) manifiestan
que el uso de plataformas con respecto a la enseñanza de la matemática
considerados bajo la autopercepción de los docentes posee mejores resultados.
De esta forma, se determinó que existe una fuerte correlación sobre el uso de
la herramienta electrónica PAM (49,8%) y GeoGebra (55,7%), mismas que colaboran
con la construcción de un aprendizaje significativo en los alumnos a partir de
la utilización de estas aplicaciones digitales interactivas, a diferencia de
las demás plataformas empleadas.
En la
investigación de Pomboza (2014) sobre “Incidencia en el aprendizaje
significativo para la educación superior” se tomó en cuenta una población de 54
estudiantes en la Escuela Superior de Chimborazo, con un nivel de confianza de
0,005 y con 27 grados de libertad, demostró que la metodología WebQuest
favorece al aprendizaje significativo dentro y fuera del aula de clases.
Por otro lado,
en el estudio realizado por Pérez (2012), acerca de la evaluación y
aprendizajes significativos con una población conformada por docentes y
estudiantes, con 3 grados de libertad y con 95% de confiabilidad, se evidencio
que el aprendizaje significativo ocurre cuando las ideas están fundamentalmente
relacionadas con lo que el alumno sabe, es decir, el conocimiento está
estrechamente relacionado con el previo.
Según Masapanta
Rivadeneira (2021) en su estudio sobre la incidencia de los procesos
atencionales en el aprendizaje significativo en 56 alumnos de nivelacion de la
carrera de Psicopedagogia mediante la prueba de B de Kendal logro determinar
que, si existe correlación entre las variables, de tal manera, con un
porcentaje mayor al 50%, los procesos atencionales se vinculan al aprendizaje
significativo, ya que le permite a los estudiantes que sus conocimientos
perduren en el tiempo.
Dimensión
|
Variables
|
Porcentaje
|
Plataformas
|
PAM
|
49,8
|
Edmodo
|
17,0
|
Moodle
|
23,3
|
Thatquiz
|
9,1
|
Geometría y Análisis
|
Derive
|
17,6
|
GeoGebra
|
55,7
|
Dr. Geo
|
4,1
|
Cabri
|
12,0
|
Mathgraft
|
8,6
|
Programación
|
Scracth
|
25,0
|
Tortugart
|
14,2
|
R
|
9,1
|
Tabla 3. Uso de plataformas y
herramientas digitales para la enseñanza de la matemática
Nota: Tabla elaborada en la investigación de
(Vaillant y Zidán, 2020)
CONCLUSIONES
El aprendizaje
significativo tiene un efecto positivo en la enseñanza de la matemática,
gracias a la elaboración de nuevos conocimientos desde los adquiridos en ciclos
educativos anteriores, ya que los estudiantes han logrado enraizar datos
matemáticos con una duración a largo plazo para mejor desenvolvimiento.
Se determinó la
correlación entre, aprendizaje significativo y enseñanza de la matemática,
porque garantiza un mayor nivel de motivación, así como aplicar conocimientos
anteriores, de esta forma, el estudiante se puede enfrentar a los retos de la
sociedad y las situaciones cotidianas.
El aprendizaje
significativo que los estudiantes de nivelación demuestran en la matemática,
permite que promuevan una mejor adaptación a los conocimientos
teóricos-prácticos.
AGRADECIMIENTOS
Los autores
agradecen a la Universidad Técnica de Ambato (UTA) y a la Dirección de
Investigación y Desarrollo (DIDE) por el apoyo brindado para la realización de
este trabajo a través del grupo de investigación PROMOCIÓN DE LA CALIDAD DE
VIDA. También queremos agradecer al proyecto de investigación GESTIÓN EDUCATIVA
Y CALIDAD DE VIDA DE LOS ACTORES DE LAS UNIDADES EDUCATIVAS DE LA COORDINACIÓN
ZONAL 3 DEL MINISTERIO DE EDUCACIÓN DEL ECUADOR, aprobado mediante Resolución
UTA-CONIN-2023-0046-R.
REFERENCIAS BIBLIOGRÁFICAS
Anzoategui, J. A. (2021). USO DE LAS MATEMATICAS. Rosario:
monografias.coom.
Baque Reyes , G. R., & Portilla Faican, G. I. (2021). El
aprendizaje significativo como estrategia didáctica para la enseñanza –
aprendizaje . Polo del conocimiento, 77-78.
Castillo , V., Yahuita , J., & Garabito , R. (2006). Estrategias
docentes para un aprendizaje significativo.
http://www.scielo.org.bo/scielo.php?pid=S1652-67762006000100015&script=sci_arttext.
González, J. E. (2020). ENSEÑANZA DE LA MATEMÁTICA. Hidalgo :
uaeh.edu.mx.
Guamán , V. (2019). El aprendizaje significativo desde el contexto
de la planificación didáctica. SciELO, 69.
López-Quijano, G. (2021). La enseñanza de las matemáticas,un reto
para los maestros del siglo XX. Colombia: Csielo.
Masapanta Rivadeneira, M. (2021). Procesos atencionales en el
aprendizaje significativo en los estudiantes de la nivelación y primero de la
carrera de psicopedagogía durante el covid – 19.
Matienzo, R. (2020). Evolución de la teoría del aprendizaje
significativo y su aplicación en la educación superior. Dialektika, 2(3),
17-26. https://doi.org/https://orcid.org/0000‐0002‐1380‐4687
Muñoz, O. E. (2020). EL CONSTRUCTIVISMO: MODELO PEDAGÓGICO PARA LA
ENSEÑANZA DE LAS MATEMÁTICAS. Colombia : educare .
Perez, Y. (2012). La evaluación por competencias y el aprendizaje
significativo. Centro de estudios de posgrado, 20-40.
Pomboza, C. (2014). WebQuest: Incidencia en el aprendizaje
significativo para la educación. Facultad de Mecánica, Escuela Superior
Politécnica de Chimborazo, 4-16.
Rivas, M. (09 de 06 de 2008). Procesos cognitivos y aprendizaje
significativo. Inspección de Educación. Madrid , Madrid , España: Printed in
Spain.
Vaillant, D., & Zidán, E. R. (28 de jul de 2020). Uso de
plataformas y herramientas digitales para la enseñanza de la Matemática.
scielo: https://doi.org/10.1590/S0104-40362020002802241
Vilchez Guizado, J., & Ramón Ortiz, J. (2022). Enseñanza
flexible y aprendizaje de la matemática en educación secundaria rural. Revista
electrónica de tecnología educativa. EDUTEC(80). https://doi.org/https://doi.org/10.21556/edutec.2022.80.2431
, María Elena
Medina Vásquez1
, Flor Abigail
Lata Morocho1
, Lady Briggitte
Yanchatipan Procel1